Use Case: Routering Landbouwverkeer
Introductie
Het Kadaster levert op reguliere basis informatie aan de provincies over verwacht landbouwverkeer in Nederland. Dit verkeer, wat veelal bestaat uit zware en grote apparaten, heeft een grote impact op de infrastructuur. Derhalve is het voor de provincie van belang een beeld te krijgen van het (groot) landbouwverkeer wat zich over het wegennet begeeft. Deze gebruiken zij vervolgens om beslissingen te maken over nieuwe wegen of het onderhoud van de bestaande infrastructuur.
Met de eigendomsgegevens van de percelen, de ligplaatsen van boerderijen en het weggennet uit de Basisregistratie Topografie (BRT) gebruikt het Kadaster een wiskundig model om de kortste route van de landbouwpercelen naar de boerderij te bepalen. Vanuit het perceel werd er eens een ‘snap’ gemaakt naar de dichtstbijzijnde weg, om daarna over de weg de kortste route te berekenen. Deze eerste stap is er één die er vaak voor zorgt dat de dichtstbijzijnde weg van het perceel wordt gevonden, maar soms zorgt deze simpele snapping er ook voor dat er onrealistische verbindingen worden gemaakt naar de weg. Deze snapping houdt namelijk geen rekening met onpasseerbare objecten zoals een spoorlijn of een rivier.
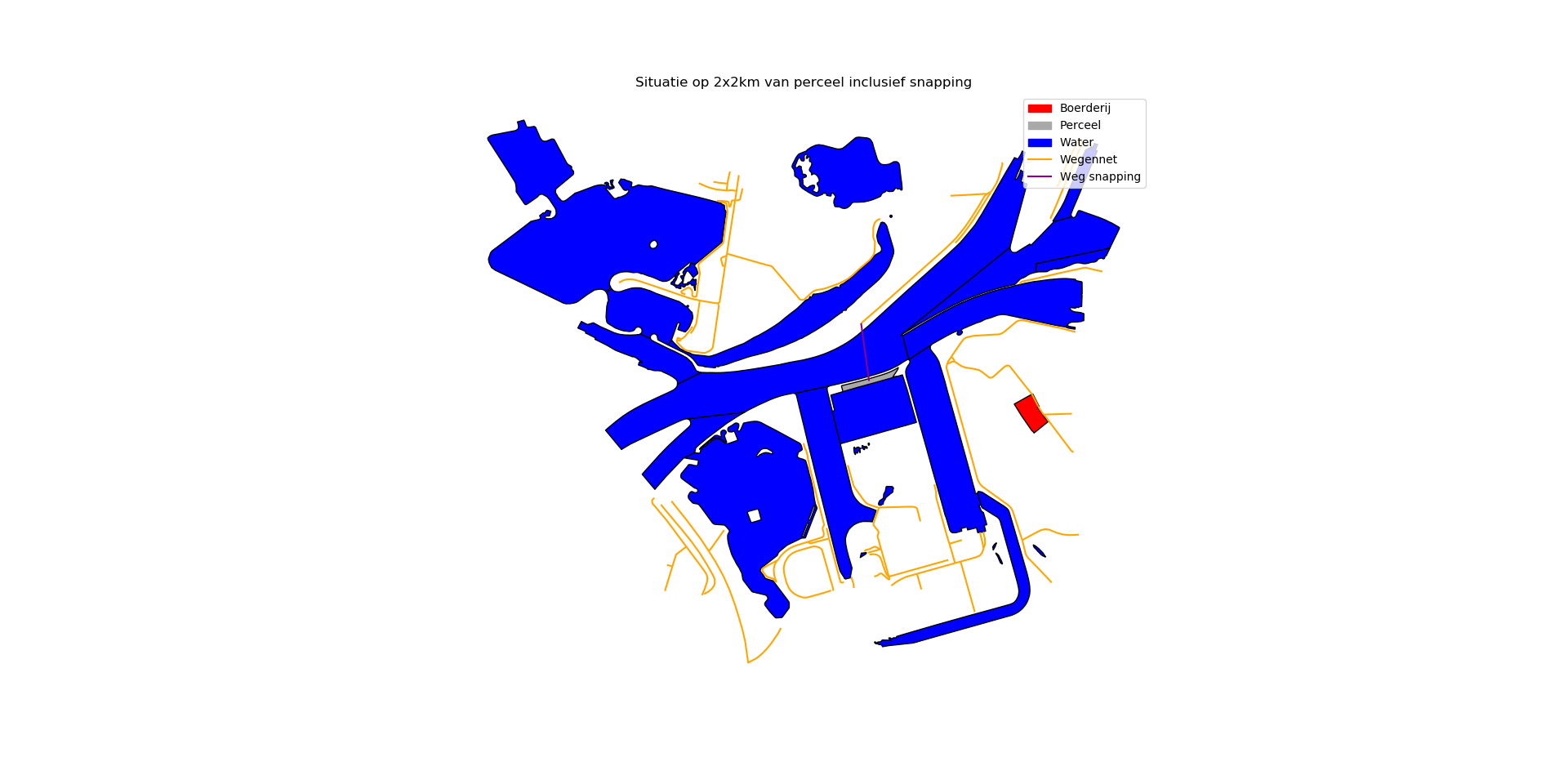
Ter illustratie, bekijk de situatie zoals getekend in Figuur 1 en Figuur 2. Deze situatie beschrijft een locatie bij de Maas, waarbij het perceel van de desbetreffende boer omringd is door water. Het perceel waarvoor de dichtstbijzijnde weg moet worden gevonden is aangegeven in het grijs. Met de huidige snapping regels wordt dit perceel toegewezen aan de weg aan de andere kant van de rivier. Onze vraag: Kunnen we de snapping regels verbeteren, op basis van wiskundige modellering/operations research technieken, om een realistischer en accurater model aan te bieden aan de provincies.
Aanpak
Het probleem zoals beschreven in de introductie is een typisch optimalisatie-vraagstuk, waarin we de kortste route van één punt naar een ander punt proberen te bepalen. Om aan te tonen dat onze aanpak werkt, bepalen we eerst de scope waarin we met dit project gaan werken.
- In eerste instantie nemen we alleen water als blokkerende factor mee. De methodiek moet echter generaal genoeg zijn om ook met andere blokkerende objecten om te kunnen gaan.
- Bij dit probleem richten we ons puur op het snappen richting de dichtstbijzijnde weg. De locatie van de boerderij wordt hierbij niet meegenomen.
We beginnen met het verzamelen en transformeren van de benodigde data. We hebben de volgende informatie nodig:
- Wat zijn de geometriën van het perceel onder consideratie?
- Wat zijn alle wegen binnen een bereik van x meter rondom dit perceel?
- Waar liggen de blokkerende factoren binnen een bereik van x meter rondom dit perceel?
Wegen en water halen we uit de Top10NL van de Basisregistratie Topografie (BRT). Hiervoor kiezen we een bounding box (selectie rondom het perceel) van maximaal 5 kilometer. Nadat we de data hebben opgehaald, schonen we hem. Daarna projecteren we een wiskundige graaf op de kaart, waarin we de hoekpunten van de geometriën (van zowel wegen, het perceel en de blokkades) aan elkaar verbinden. Omdat we het projecteren op een 2D veld, zal de optimale oplossing altijd over deze hoekpunten gaan.
Shortest Path Problem (SPP): De optimale route van A naar B
Bovenstaand scenario beschrijft een single-source shortest path problem, waarbij we de kortste route van het startpunt (hier: het perceel) willen vinden naar één eindpunt (hier: de weg) willen vinden. In deze use case bekijken we enkele geometrische technieken om van onze kaarten tot een wiskundige graaf representatie te komen en met een combinatie van bekende optimalisatie modellen zoals Dijkstra’s algoritme en het A-Ster algoritme tot een optimale oplossing te komen, in niet al te lange tijd.
Data Cleaning
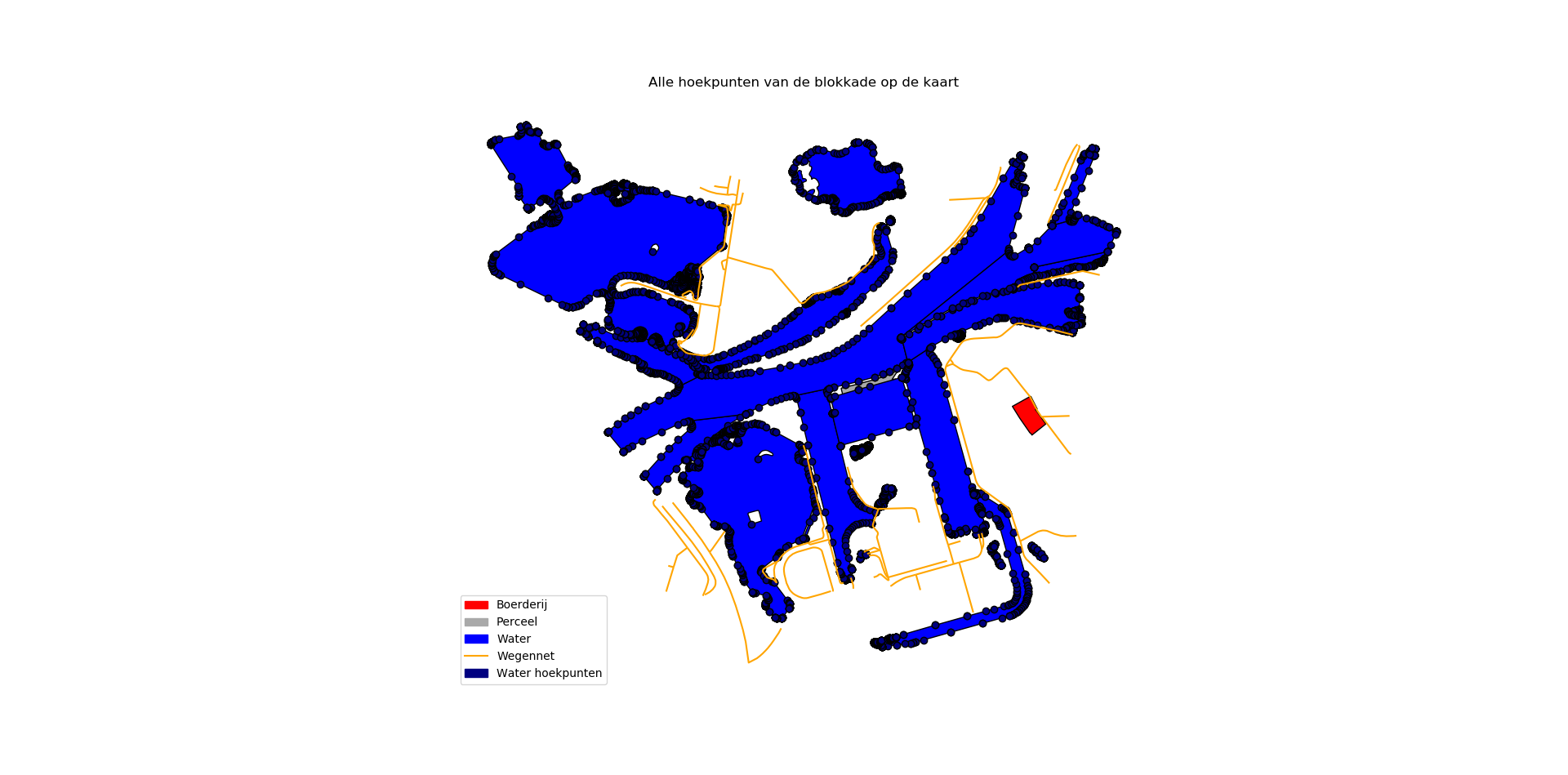
Zoals met bijna iedere data-gedreven oplossing zal er eerst data cleaning moeten worden toegepast. Ter illustratie, wanneer we alle hoekpunten van het water visualiseren op de huidige input, krijgen we een kaart zoals in Figuur 3. Hier komen twee duidelijke uitdagingen naar boven:
- Doordat de data van de BRT dusdanig precies is zijn alle rondingen van het water goed vastgelegd. Dit betekent echter ook dat er soms op enkele meters meerdere hoekpunten te vinden zijn. Dit zorgt ervoor dat de hoeveelheid mogelijke routes exponentieel toeneemt.
- De polygonen van het water liggen tegen elkaar aan of laten zelfs een kleine ruimte over. Dit zorgt ervoor dat het soms lijkt alsof er een route tussen de punten te vormen is, terwijl dit in de realiteit niet zo is.
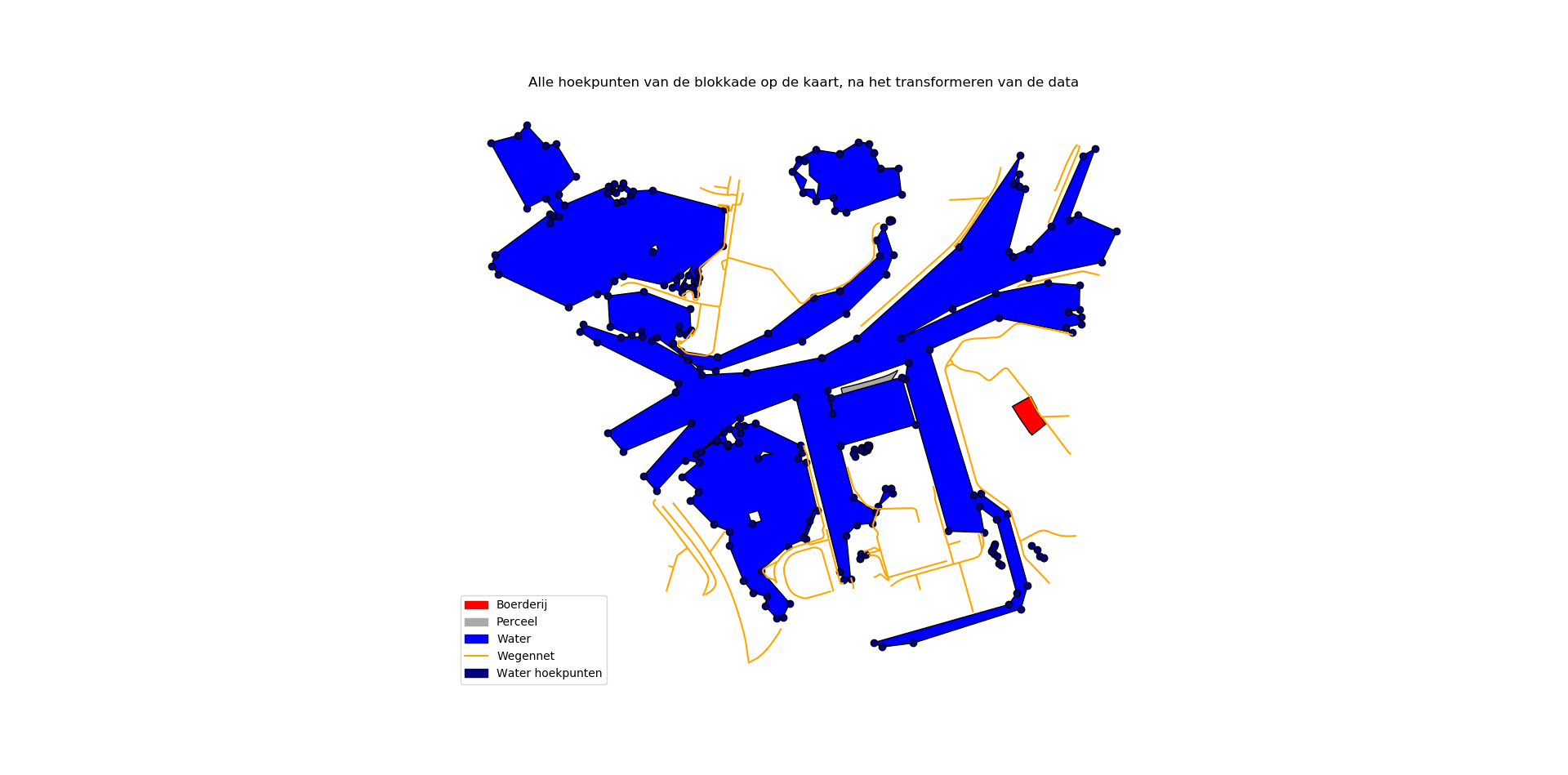
Om beide uitdagingen aan te pakken passen we twee manieren toe om de data op te schonen. Om ervoor te zorgen dat polygonen die zeer dichtbij elkaar liggen overlappen passen we een buffer toe. Hierbij moeten we oppassen de buffer niet te groot te nemen, om te voorkomen dat polygonen over wegen komen te liggen die wel degelijk bestaan. (Denk aan bruggen waarover landbouwvoertuigen wel mogen gaan.) Ten tweede gebruiken we een algoritme om de blokkerende polygonen te simplificeren. Dit is een algoritme waarmee overbodige bochten worden verwijderd, maar de originele topology zoveel mogelijk behouden wordt. Dit verlaagt de hoeveelheid hoekpunten waar het routeringsalgoritme mee moet omgaan met een significante hoeveelheid. Hiermee verliezen we wel enige accuraatheid voor de uiteindelijke oplossing. Echter, omdat de originele topologie behouden is, gaan er geen doorgangroutes verloren en verschuiven ze hooguit enkele meters ten opzichte van de realiteit. Nadat de data opgeschoond is krijgen we de kaart zoals afgebeeld in Figuur 4.
Optimalisatie
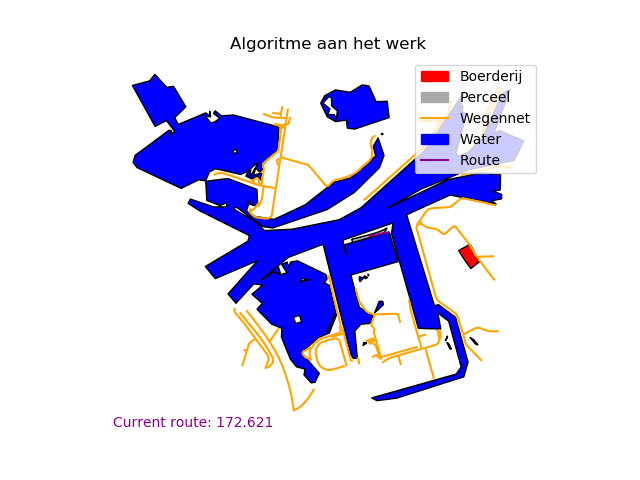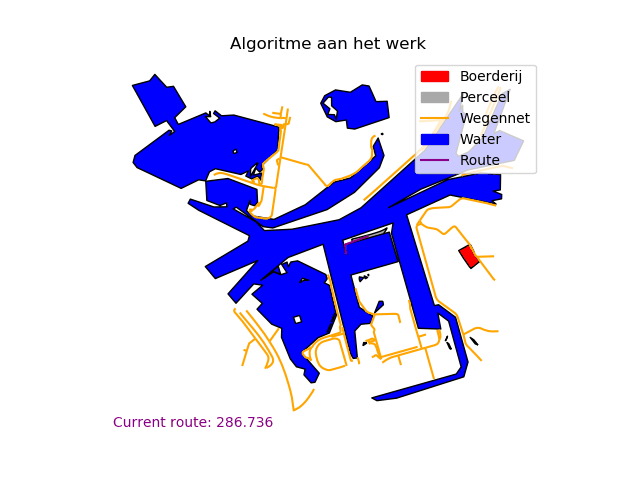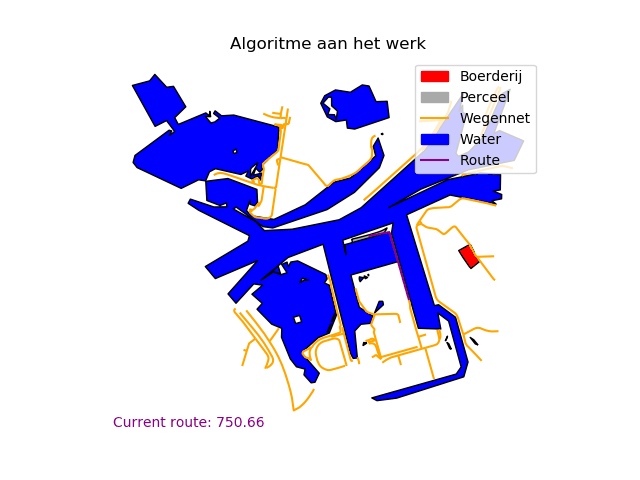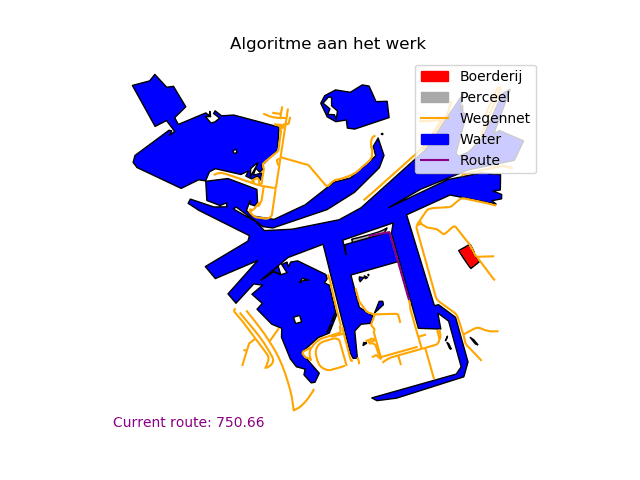
De data is nu klaar om te transformeren in een wiskundige graaf en te optimaliseren met (bestaande) algoritmen. We construeren de graaf door het startpunt en alle hoekpunten als nodes te evalueren en verbindingen te berekenen op basis van de euclidische afstand. Indien deze verbinding door een blokkade (i.e. water) gaat is er geen verbinding tussen deze punten. Echter, om van tevoren alle mogelijke verbindingen tussen alle hoekpunten te berekenen is een computrationeel zwaar probleem, waar veel tijd in gaat zitten. In plaats daarvan bouwen we de graaf procedureel op vanuit ons startpunt, om uiteindelijk met zo min mogelijk stappen bij een weg uit te komen. Hiervoor gebruiken we een variant op het A-Ster algoritme. Startend bij het perceel onder consideratie evalueren we alle aanliggende punten. Hierbij bekijken we de daadwerkelijke kortste afstand van het pad tot nu toe en de kortst mogelijke afstand tot een weg (de euclidische afstand naar de dichtstbijzijnde weg, ongeacht eventuele blokkades). Een visualisatie van het algoritme vind je in Figuur 5.